Plus: How do you generate a random sample of triangles? and: How can you measure the distance between two triangles

Whenever you want to model something, say a physical system like the tumbler and pins in a door lock or a robotic arm, it's helpful to think of each possible state of the system as a point in a space. This can help if you want to find a way to get from one state to another (e.g. planning a path for the robotic arm), or if you want to know how likely a state is if you randomly sample a space (e.g. vibrating a lock to try to pick it). Usually it's best to try to find a good representation and build up from there. To illustrate the process, we'll take an extremely simple example—triangles—and work through each step.

Representing Triangles

The naive way to do this is just to represent the triangle as three points in a plane. The problem with this is that many triangles which we should consider the same have different representations:

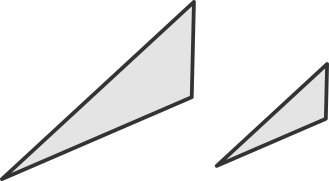
a picture of two triangles of the same shape but two different sizes

So we can have triangles of the same shape be different sizes or in different positions and so have a different set of representative points. Ideally our representation would be unique for a particular shape of triangle regardless of the size or position we see the triangle in.

If you remember from trig class, the internal angles of every triangle add up to exactly 180°. That means we could represent a triangle by its angles to avoid the issues of varying size and position. So we can use a list of three angles and all we have to do is to make sure they add up exactly to 180°.

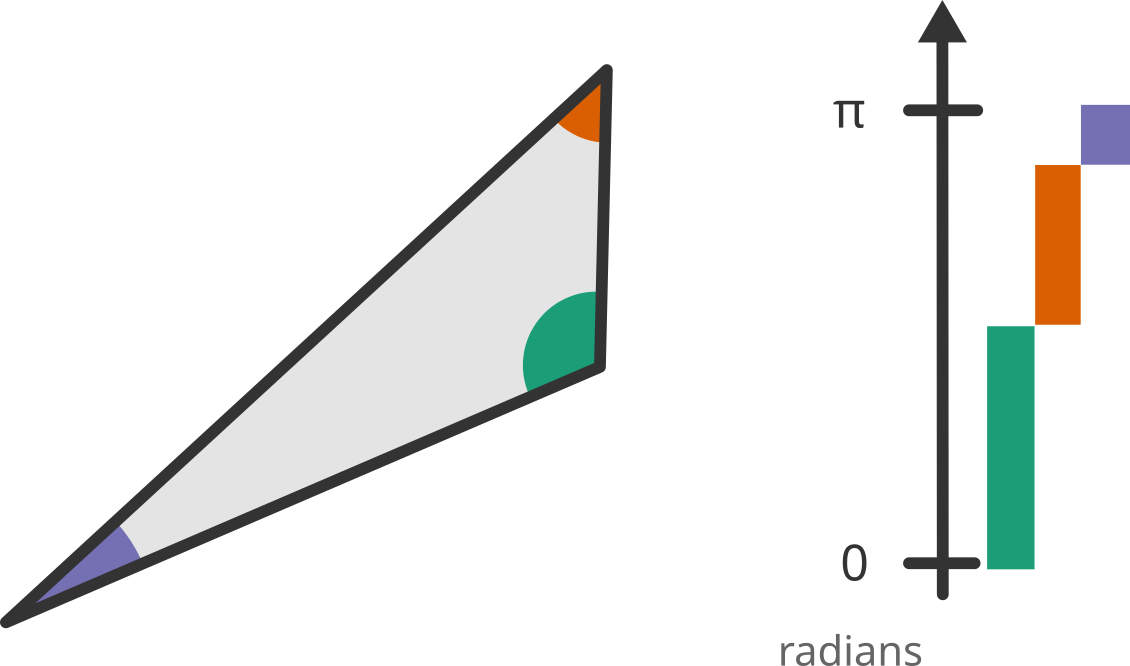
A triangle with the three angles colored to match their opposite sides; Next to it three colored bars set end-to-end with the total measure being 180°

The Space of Triangles

Now that we have a representation for all triangles we can think about what the space they form looks like. Since we have three numbers for a representation, we can associate any possible value of our representation with a point in 3D space. And since the numbers must add up to 180°, we don't use the entirety of our space (because not all points have coordinates that add up to 180). Also, angles are always positive, so we'll only be using the octant of space where all coordinates are positive.

It may take a little legwork, but it should be possible to work out that the shape this makes is a triangle with one vertex on each axis where that axis equals $\pi$ (also known as a simplex):

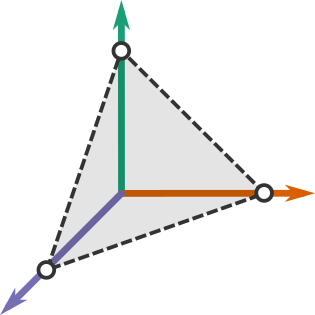
as described

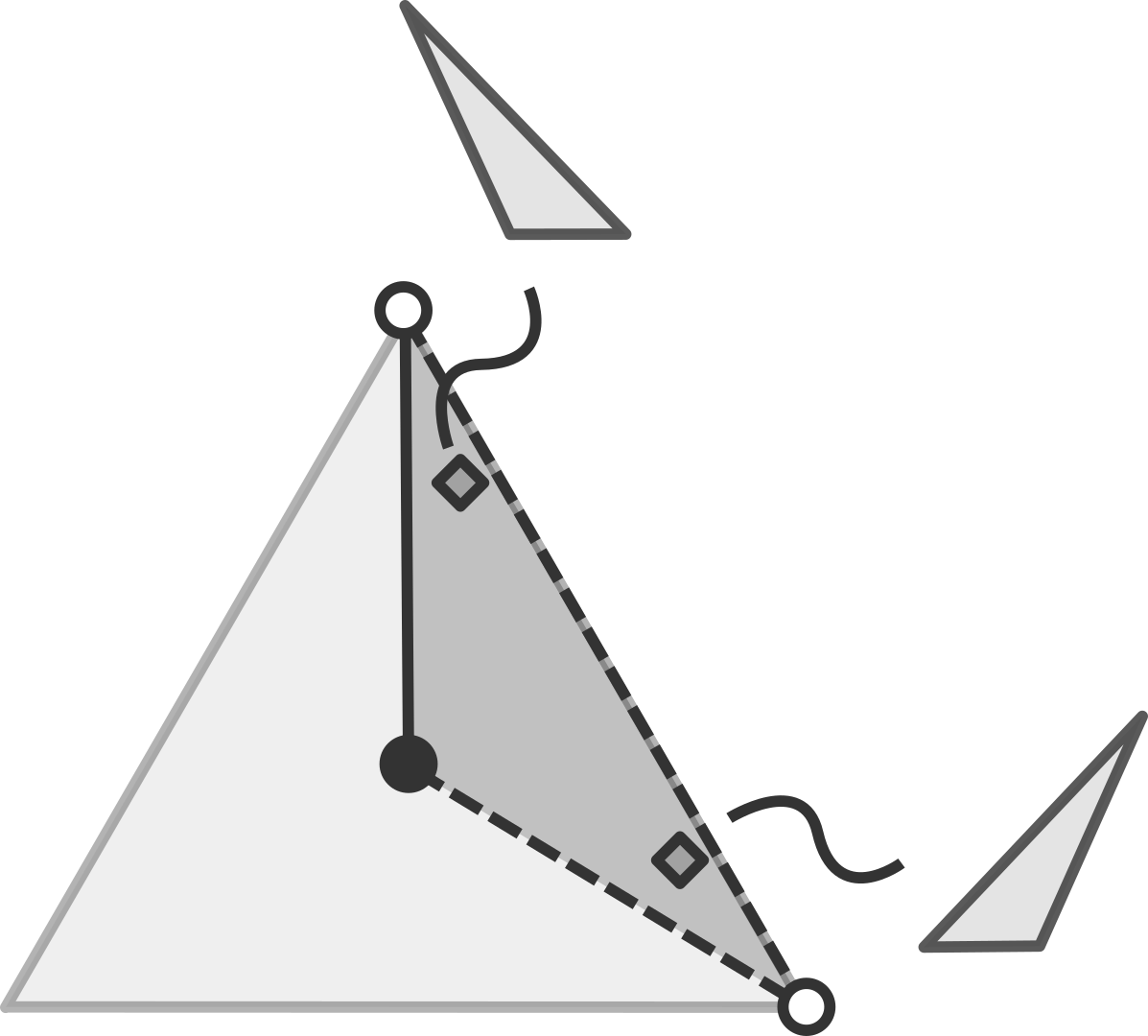
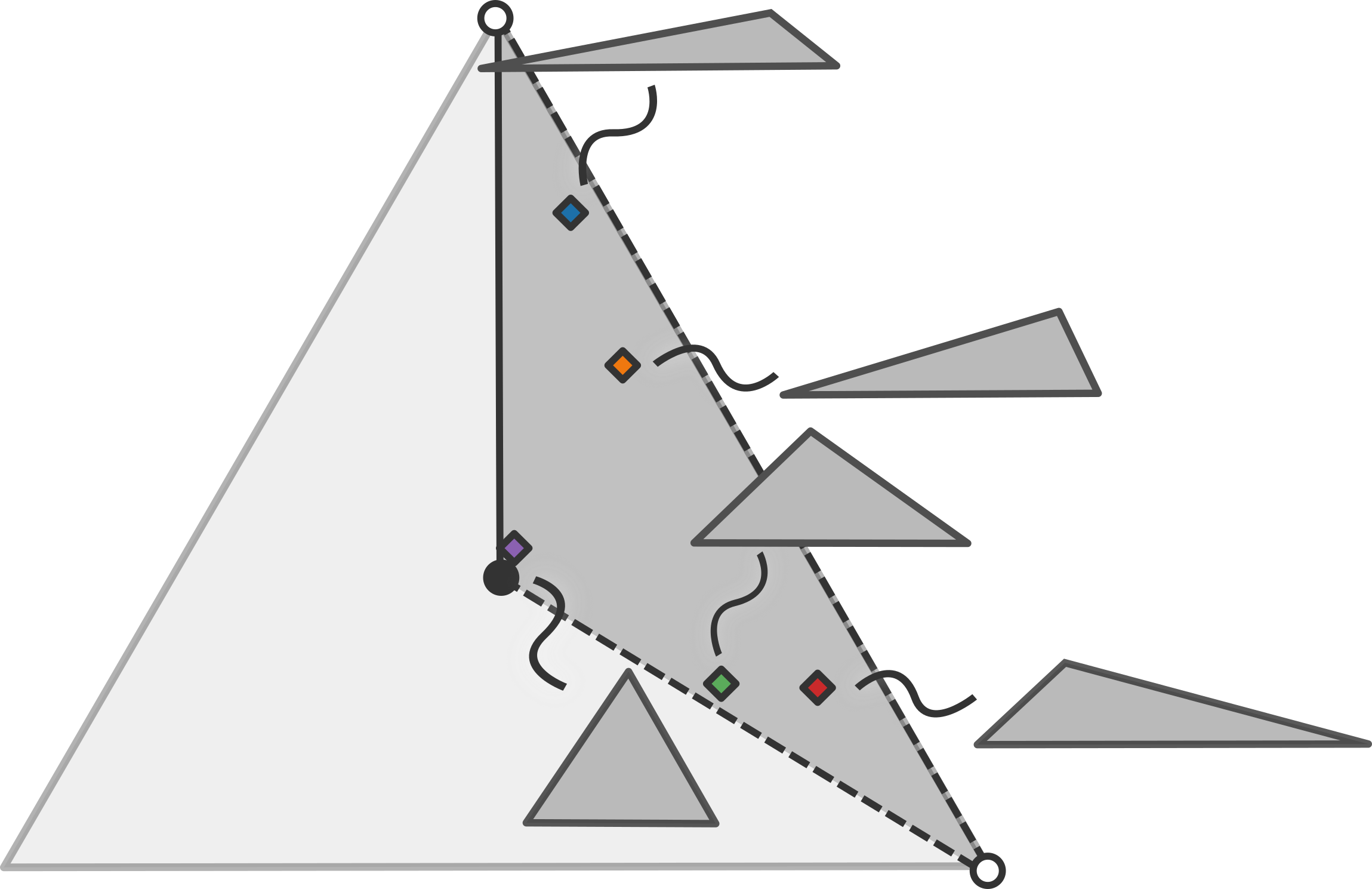
So here we see a space where each point represents a triangle. However, there's one snag. If we look at what triangles are represented where, we see that any triangle can be represented by three different points:

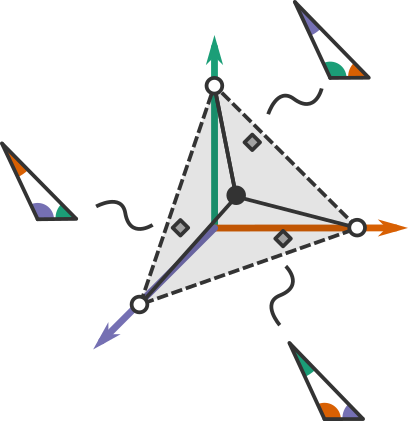
the space of triangles with three points highlighted each in symmetric with the others by 120° rotation. Each point is shown with the associated triangle it represents and the triangles are the same shape, just rotated

To deal with this situation, we only need to restrict our space to one third of the original space such that we treat the corresponding points in the other thirds as equivalent:

The simplex is divided into thirds with the divisions running from the center to each vertex. The thirds are then shown stacked on top of each other with a line piercing through each to show the equivalence of the points it passes through

In terms of our coordinates this simply means that we make sure the first coordinate is the smallest of the three.

Measuring the Space

Now that we know what the space of triangles looks like, we can go ahead and calculate what its size is. First we can see that the long edge of the space forms a triangle with the two axes it is closest to, which means it must be $\pi \sqrt{2}$ long.

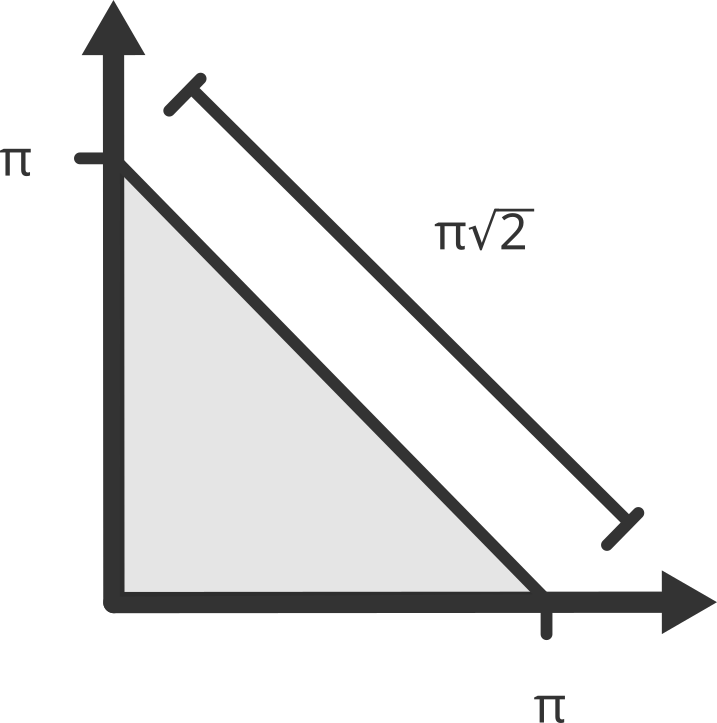
Two axes with a diagonal that intersects at π on both which makes it a length of π * sqrt(2)

And since the formula for the area of an equilateral triangle is given by $\frac{\sqrt{3} l^2}{4}$ where $l$ is the length of one of the sides, we have the area for our space (remembering it is one-third of the equilateral triangle):

$$\frac{\pi^2 \sqrt{3}}{6}$$

It's weird seeing a $\pi^2$, but since we're calculating area in a space whose dimensions are angles that's somewhat bound to happen.

So what does this value mean? Not much by itself, but now that we've gone this far there are a couple of other questions that come to mind:

How Can You Randomly Choose a Triangle?

Often it's useful to be able to randomly sample a space. This can be for generating test cases or examples, for optimization (used in some metaheuristic methods), or even for statistical mechanics. So if for nothing else than practice, let's see how to generate random samples in our space of triangles.

The idea of the sampling is to generate samples in a space we know how to (such as a square) and then transform that into the space we want. Our approach will be to start by sampling a square (just by sampling two random variables $[0,1)$), which we'll call $u$ and $v$. Then we'll reflect the samples about the diagonal (just by making $u$ always be the smaller sample) so that the sampling space is a triangle. Then we need to transform that triangle so that it coincides with the space we've described. After banging your head against some linear algebra for a while, you should arrive at these equations:

$$a = \frac{-u + v + 1}{3} \pi$$

$$b = \frac{2 u - v + 1}{3} \pi$$

$$c = \frac{u - v}{3} \pi$$

Where $a$, $b$, and $c$ are the angles of the triangle. Here's an implementation of sampling:

import random

def sample_triangles():
    u = random.random()
    v = random.random()

    # We want to sample a triangle, not a rectangle
    if (v > u):
        u,v = v,u

    a = np.pi * (-u + 3 * v + 1) / 3
    b = np.pi * (2 * u - 3 * v + 1) / 3
    c = np.pi * (1 - u) / 3
    return a,b,c

Note that this code might not deal properly with edge-cases. It's merely for illustration

Now with code to generate samples we can display some examples of what it generates:

import numpy as np
import matplotlib.pyplot as plt

# Generate a consistent sample set
random.seed(1)

triangles = []

for i in range(5):
    a_ang,b_ang,c_ang = sample_triangles()

    triangles.append([a_ang, b_ang, c_ang])

    # c must be largest angle so longest edge is down

    if (a_ang == np.max([a_ang, b_ang, c_ang])):
        a_ang,b_ang,c_ang = b_ang,c_ang,a_ang

    if (b_ang == np.max([a_ang, b_ang, c_ang])):
        a_ang,b_ang,c_ang = c_ang,a_ang,b_ang

    print(f"a: {a_ang:0.2f}, b: {b_ang:0.2f}, c: {c_ang:0.2f}")

    b_len = np.sin(b_ang) / np.sin(c_ang)

    x = b_len * np.cos(a_ang)
    y = b_len * np.sin(a_ang)

    triangle_vertices = np.array([[0, 0], [1, 0], [x, y]])

    triangle = plt.Polygon(triangle_vertices, edgecolor='#333333', facecolor='#00000020', linewidth=5, joinstyle='round')

    plt.figure()
    plt.gca().add_patch(triangle)
    plt.axis('scaled')
    plt.gca().set_axis_off()
    plt.show()

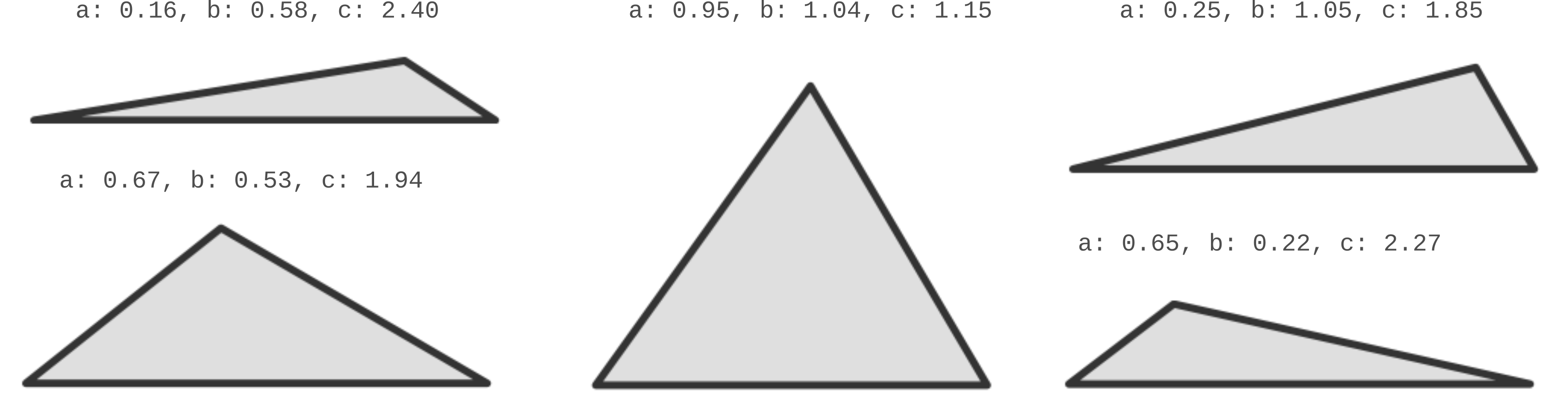
Five randomly generated triangles

Now that we have some examples, there's one more question we might like to answer:

How Can You Measure the Distance Between Two Triangles?

Since we have a representation of triangles in a euclidean space, measuring the distance between them should be trivial, we just have to take the euclidean distance between their points:

$$distance = \sqrt{(a_1 - a_2)^2 + (c_1 - c_2)^2 + (c_1 - c_2)^2}$$

However, there's one more wrinkle. Here we have some points in triangle space, and if you look at the points on opposite ends, you see that they are actually very similar despite being far apart.

A depiction of triangle space with specific points labelled with the shape of triangle they represent. On the far sides of the triangle we see that mirror images of a triangle are actually very similar

This makes sense because the other two parts of the original representation space directly abut these edges so we should expect a continuous transition across those edges. And the reason we only kept one third of the original space was because all three were identical, so the triangles across that edge are in fact the same ones as those on the opposite end of our space.

This means we can move across that edge and wrap over to the other side. It might be better to visualize by rolling up the space into a cone:

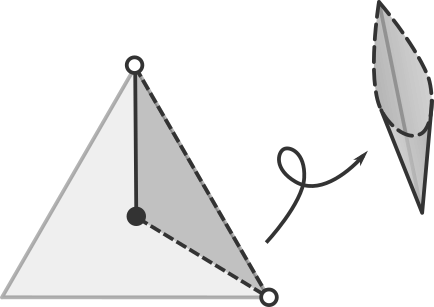
The flat space of triangles is rolled up into a cone

So, given this, how would we calculate the distance taking into account that points may be closer to each other across the joining edge? A straightforward approach is to take the points we're comparing and rotate them $2 \pi / 3$ to one of the other thirds of the simplex. Then we find the shortest distance of the distances between each pair.

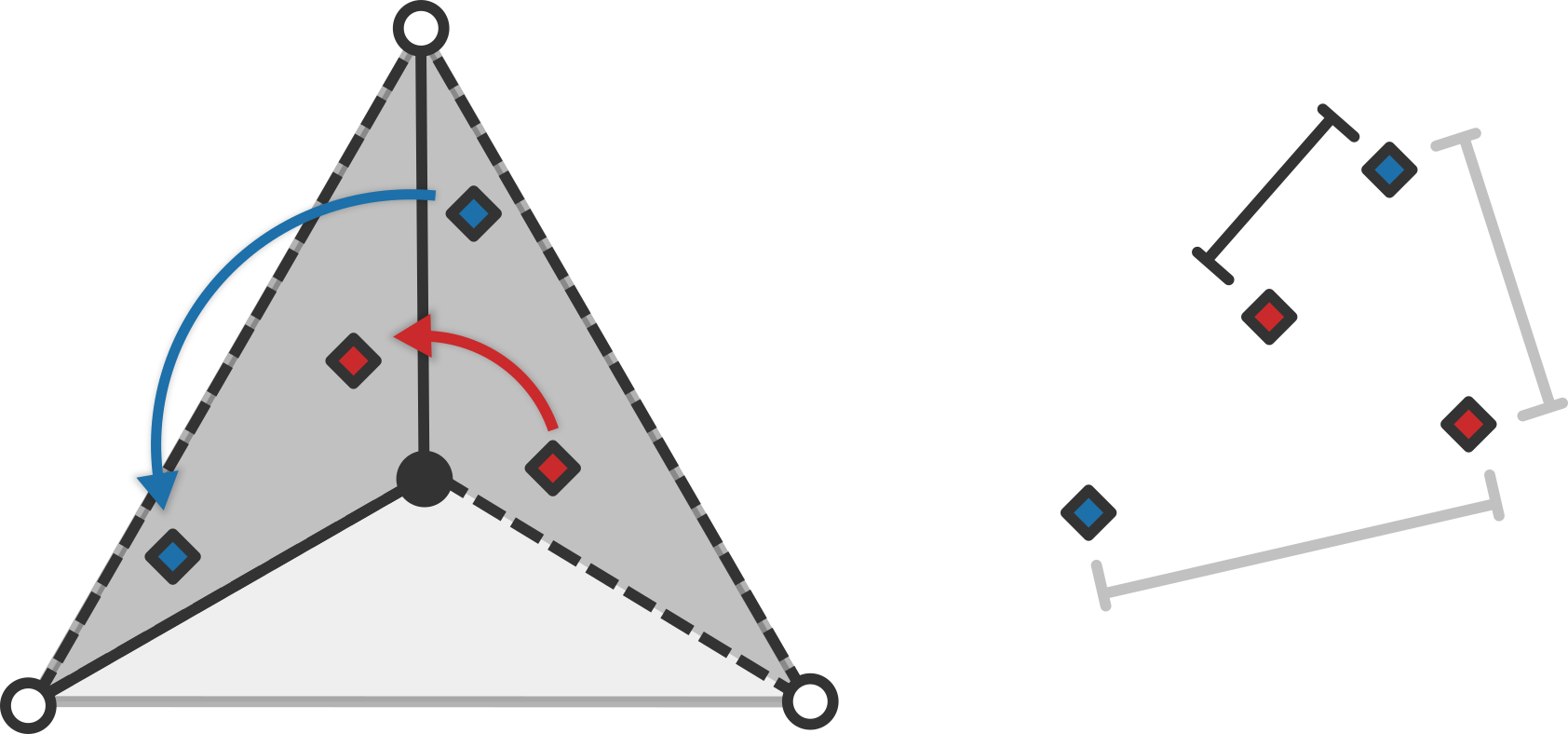
Comparing two points by rotating the points 2*pi/3 and comparing each pair

Because the simplex is symmetric with respect to all three axes, rotation is just as simple as rotating the coordinates.

$a' = b$

$b' = c$

$c' = a$

def triangle_dist(T1, T2):
    T1_rotated = np.array([T1[2], T1[0], T1[1]])
    T2_rotated = np.array([T2[2], T2[0], T2[1]])

    return min(np.linalg.norm(T1 - T2), np.linalg.norm(T1 - T2_rotated), np.linalg.norm(T1_rotated - T2))

So now we can get the exact distances between the triangles we sampled before. First we just plot them in the space:

A view of triangle space with the five triangles we sampled previously called-out

And then we rotate all the points to another section to see what the actual distances are (remembering that the length of the long edge of the space is $\approx 1.41\pi$):

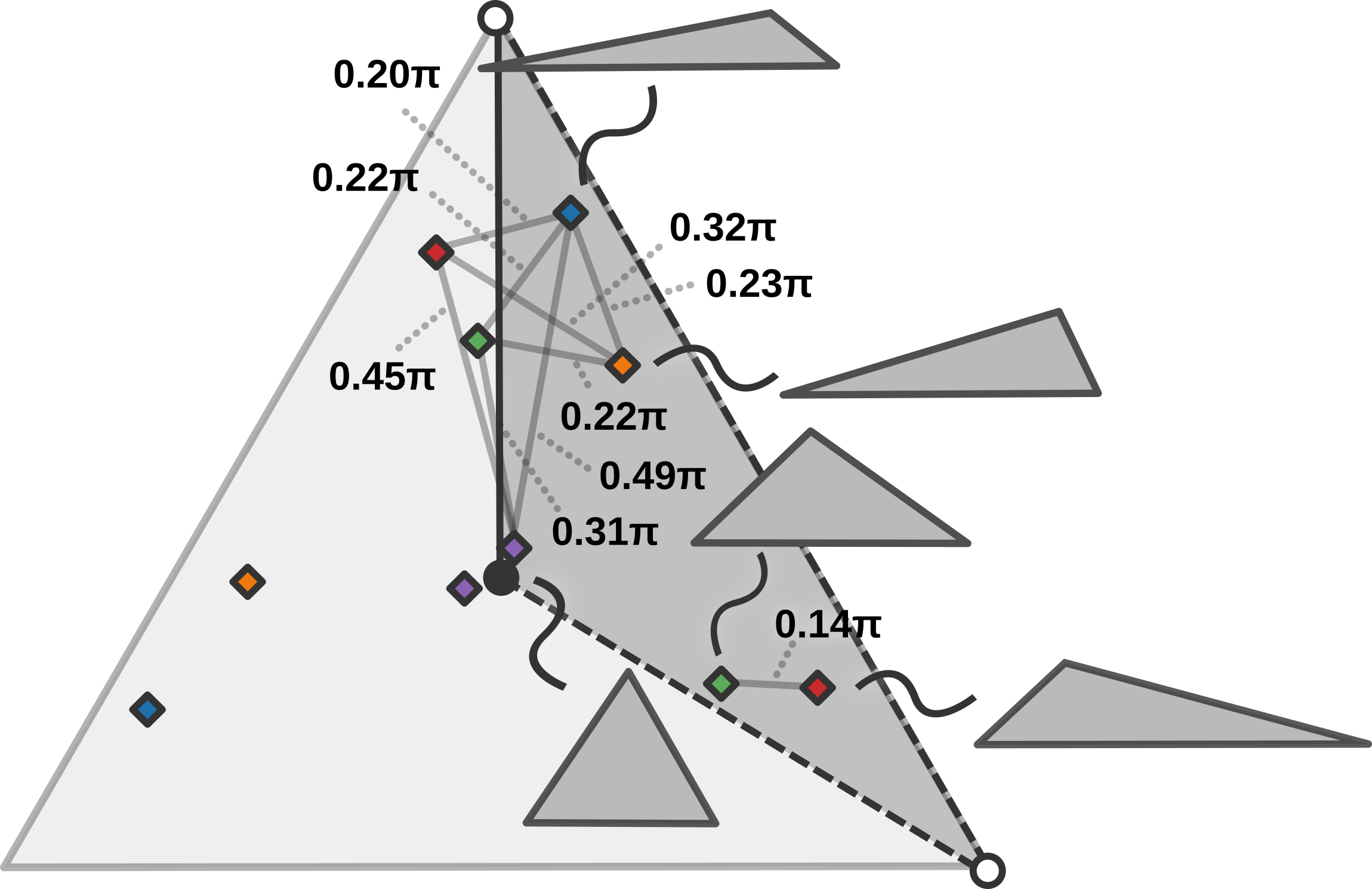
Same as above but with distances between all five triangles labelled

Conclusion

If you're wondering what the point of all this is, then, realistically, it was mostly just for fun. But each of these questions are ones that we might want to ask about other concepts and spaces, so it might be useful to have a simple but non-trivial example which answers those questions.

A Map for the Space of Triangles

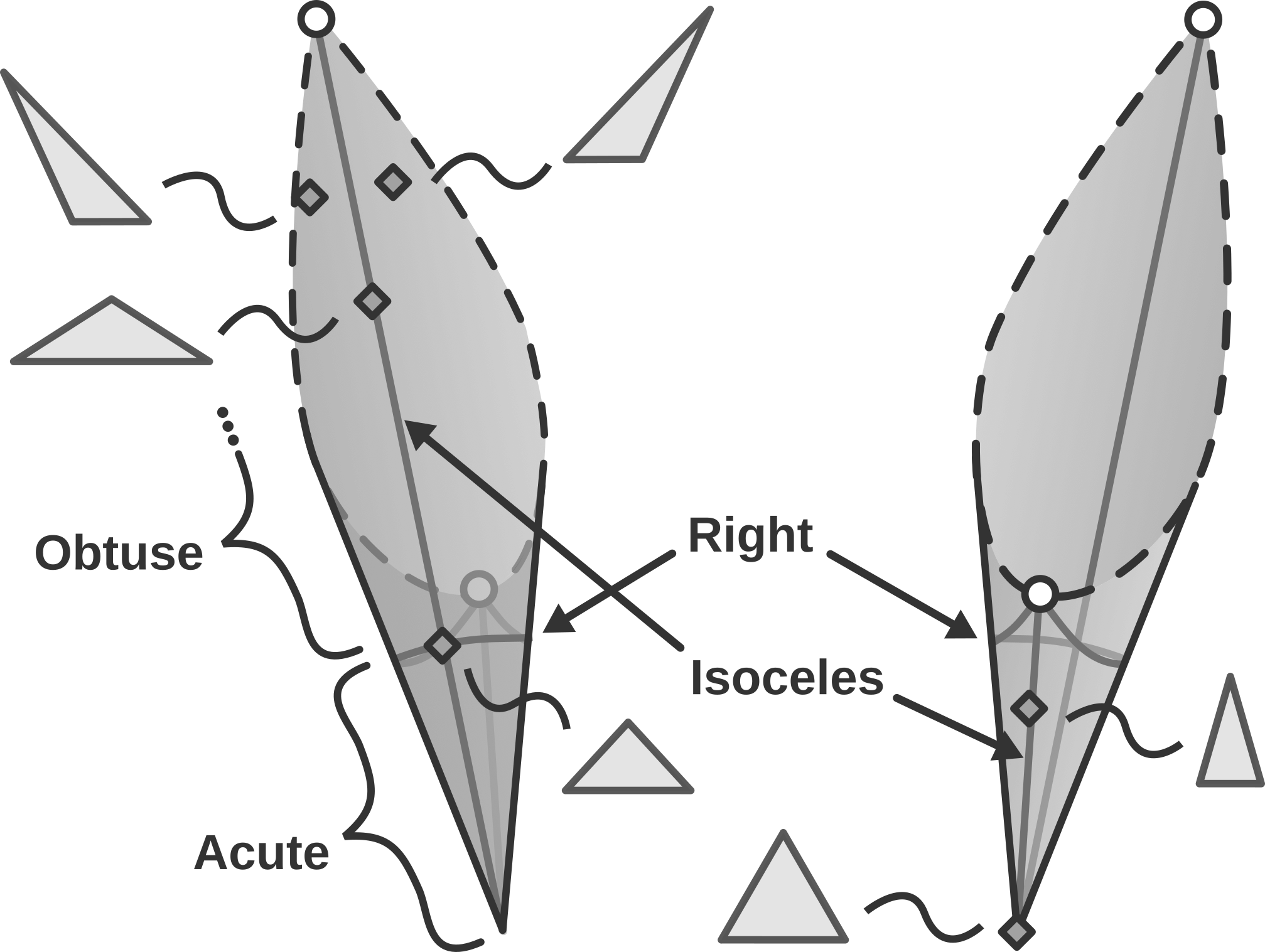
A diagram of the cone representing all triangles with several points and types of triangles labelled

Update 2023-09-23

Some other treatments of the idea:

J. Gaspar and O. Neto, All triangles at once, Amer. Math. Monthly 122 (2015), 982-982.
I. Stewart, Why do all triangles form a triangle?, Amer. Math. Monthly 124 (2017), 70-73.